Given,
The number of total students and faculty is 213.
From the table,
The number of students opposed to the change is, n(student oppose) = 44.
The number of faculty members opposed to the change is, n(faculty oppose) = 20.
The number of faculty members favor to the change is, n(faculty favour) = 11.
The probability of elected person is a student oppose to the change or faculty member either for or against is,
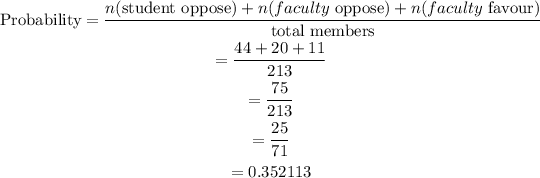
Hence, the probability is 25/71.