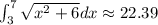Answer: 22.39
Given:
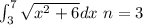
The trapezoidal rule states that:
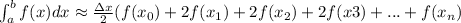
Where:
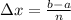
From the given, we know that:
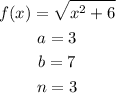
With this, we know that:
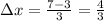
We will then divide the interval [3,7] into n=3 subintervals of 4/3, which will give us:
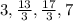
Now, we will evaluate the function at these endpoints:
![\begin{gathered} f(x)=√(x^2+6) \\ \Rightarrow f(3)=√((3)^2+6)=√(15) \\ \operatorname{\Rightarrow}2f((13)/(3))=2\sqrt{((13)/(3))^2+6}=(2√(223))/(3) \\ \operatorname{\Rightarrow}2f((17)/(3))=2\sqrt{((17)/(3))^2+6}=(14√(7))/(3) \\ \Rightarrow f(7)=√((7)^2+6)=√(55)\frac{}{} \end{gathered}]()
We will then sum up the values and multiply by Δx/2:
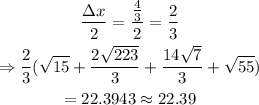
Therefore,