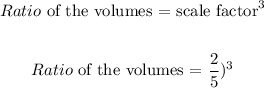Question

Given the ratio of the sides of twosimilar figures is 2/5, what is theratio of the volumes?

Answer 1

Answer:

The ratio of the volumes is 8/125

Step-by-step explanation:

Given:

The ratio of the sides of two similar triangles = 2/5

To find:

the ratio of the volumes

The ratio of the sides (length) of similar shapes is known as the scale factor

`\begin{gathered} Scale\text{ factor = }\frac{length\text{ of one side}}{length\text{ of its corresponding sides}} \\ \\ scale\text{ factor = }(2)/(5) \end{gathered}`

The volume of the ratio is the cube of the scale factors

To get the ratio of the volumes, we will cube the ratio given:

`\begin{gathered} Ratio\text{ of the volumes = \lparen scale factor\rparen}^3 \\ \\ Ratio\text{ of the volumes = \lparen}(2)/(5))^3 \end{gathered}`
`\begin{gathered} Ratio\text{ of the volumes = }(2^3)/(5^3) \\ \\ Ratio\text{ of the volumes = }(8)/(125) \end{gathered}`