Given:
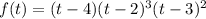
Required:
We need to find the long run behavior.
Step-by-step explanation:
Recall that the long-run behavior of a polynomial function is determined by its leading term.
Consider the given polynomial function.
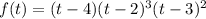
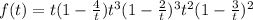
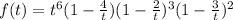
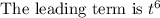
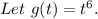
Take the limit as infinity.
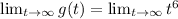
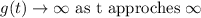
Take the limit as negative infinity.
![\lim_(t\to-\infty)g(t)=\operatorname{\lim}_(t\to-\infty)t^6]()
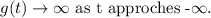
Hence we get
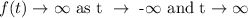
Final answer:
The long run behavior is infinity.