SOLUTION
Given the question in the image, the following are the solution steps to complete the table
STEP 1: Write the equation of the line

STEP 2: Calculating the residual when x=10
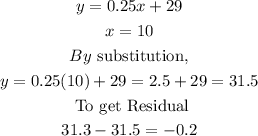
STEP 3: Calculating the residual when x=20
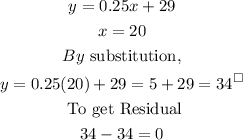
STEP 4: Calculating the residual when x=30
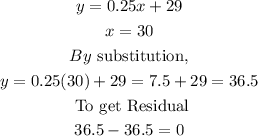
STEP 5: Calculating the residual when x=40
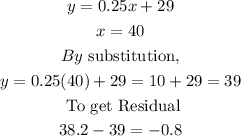
STEP 6: Plotting the quality of fit graph
A residual plot has the Residual Values on the vertical axis; the horizontal axis displays the independent variable. A residual plot is typically used to find problems with regression. A residual is a measure of how well a line fits an individual data point. This vertical distance is known as a residual. For data points above the line, the residual is positive, and for data points below the line, the residual is negative. The closer a data point's residual is to 0, the better the fit.
We have the table below:
This table for plotting the residuals gives the graph below: