Question

I need to know how to do this problem and graph it on a graph like this one below…Problem: Makayla earns $7 per hour at the bagel shop and $12 per hour mowing lawns. Makayla needs to earn at least $120 per week, but must work less than 30 hours per week. Write and graph the system of linear inequalities that describes this situation. Graph:

Answer 1

Given that:

- Makayla earns $7 per hour at the bagel shop and $12 per hour mowing lawns.

- She needs to earn at least $120 per week, but must work less than 30 hours per week.

Let be "x" the number of hours Makayla works in the bagel shop, and "y" the number of hours she works in the mowing lawns.

Using the information given, you can set up the following System of Linear Inequalities:

`\begin{cases}7x+12y\ge120 \\ x+y<30{}\end{cases}`

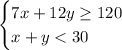
The first inequality means that she needs to earn at least $120 per week, and the second inequality means that she needs to work less than 30 hours per week.

You can rewrite each equation by solving for "y":

- For the first inequality:

`\begin{gathered} 12y\ge-7x+120 \\ \\ y\ge-(7)/(12)+(120)/(12) \\ \\ y\ge-(7)/(12)x+10 \end{gathered}`

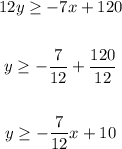
- And for the second inequality:

`y<-x+30`

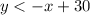
Notice that the boundary line of the first inequality is:

`y=-(7)/(12)x+10`

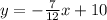
It is written in Slope-Intercept Form:

`y=mx+b`

Where "m" is the slope and "b" is the y-intercept.

Notice that, for the first line:

`\begin{gathered} m_1=-(7)/(12) \\ \\ b_1=10 \end{gathered}`

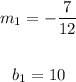
The slope indicates that the lines move 12 units to the right and 7 units down.

Since the symbol of the inequality is:

`\ge`

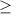
The line is solid and the shaded region is above the line.

The boundary line of the second inequality is:

`y=-x+30`

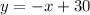
Notice that:

`\begin{gathered} m_2=-1 \\ b_2=30 \end{gathered}`

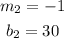
Since the symbol is "Less than", the line is dashed and the shaded region must be below the line.

Now you can graph the System of Linear Inequalities.

Hence, the answer is:

- System of Linear Inequalities:

`\begin{cases}7x+12y\ge120 \\ x+y<30{}\end{cases}`

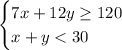
- Graph: