Question

How long will it take for your money to double if you invest $12,500 at an interest rate of 9% compounded continuously? Round your answer to the nearest tenth, and be sure to label your answer.

Answer 1

In order to calculate the interest rate compounded continuously, we can use the formula:

`A=P\cdot e^(rt)`

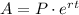
Where A is the final amount after t years, P is the principal and r is the interest rate.

So, using A = 2P, P = 12500 and r = 0.09, we have:

`\begin{gathered} 2P=P\cdot e^(0.09\cdot t) \\ 2=e^(0.09t) \\ \ln (2)=\ln (e^(0.09t)) \\ 0.693=0.09t\cdot\ln (e) \\ 0.693=0.09t \\ t=(0.693)/(0.09) \\ t=7.7 \end{gathered}`

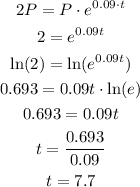
It will take 7.7 years to double the initial investment.