We have that the 80% of this type of seeds germinate, if we plant 90 seeds, the 80% is:
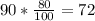
Then we know that 72 seeds will germinate.
a) The probability that fewer than 75 seeds germinate is 1 or 100%, having in count that at least 72 seeds will germinate.
Then the correct answer is 1 (100%)
b) The probability of 80 or more seeds germinating is 0, again, having in mind the percent of seeds that germinate. In other words, as just 72 of 90 seeds will germinate, it's impossible that 80 or more seeds will germinate.
Then the correct answer is 0 (0%).
c) To approximate the probability that the number of seeds germinated is between 67 and 75 is the average of the probability that 67 seeds have been germinated and the maximum probability because 72 are the seed that will germinate.
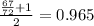
Then the correct answer is 0.965