Given:
mean(μ) = 100
SD (σ) = 15.
Find: the IQ interval that covers the middle 80%
Solution:
The middle 80% would cover 40% to the right and 40% to the left of the mean.
Using the standard normal distribution table, locate the z-value that covers 40% from the center.
Based on the table, the z-value that covers 40% from the center is +1.282 to the right and -1.282 on its left.
Now, to get the exact IQ values located on these z-values, let's use the formula below.
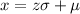
Let's plug into the formula above, mean(μ) = 100 and SD (σ) = 15.
At z = 1.282,
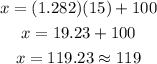
At z = -1.282,
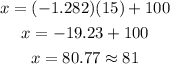
Therefore, the middle 80% of IQs fall between 81 and 119.
x₁ = 81
x₂ = 119