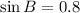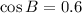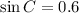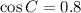Question

How would I find sin B, Cos B, sin C, and Cos C

Answer 1

The given triangle is

We get hypotenuse =BC=40 by observing the given triangle.

Consider the angle B.

For angle B, the Opposite side is AC=32 adjacent side AB =24.

We know that

`\sin \theta=\frac{Opposite\text{ side}}{\text{Hyponetuse}}`

`\sin B=(AC)/(BC)`

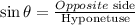
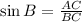
Substitute AC=32 and BC=40, we get

`\sin B=(32)/(40)=0.8`

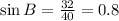
We know that

`\cos \theta=\frac{adjacent\text{ side}}{\text{Hypotenuse}}`

`\cos B=(AB)/(BC)`

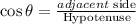
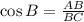
Substitute AB=24 and BC=40, we get

`\cos B=(24)/(40)=0.6`

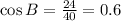
Consider the angle C.

For angle C, the Opposite side is AB=24 and the adjacent side AC=32.

`\sin C=(AB)/(BC)`

Substitute AB=24 and BC=40, we get

`\sin C=(24)/(40)=0.6`

`\cos C=(AC)/(BC)`

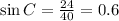
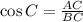
Substitute AC=32 and BC=40, we get

`\cos C=(32)/(40)=0.8`

Hence the answers are

`\sin B=0.8`

`\cos B=0.6`

`\sin C=0.6`

`\cos C=0.8`