Question

I need help with this math problem please. I have tried many times but still have not figured out the correct answers for each lengths.

Answer 1

To determine if a set of three lengths can be a triangle you have to check the rule of the sides of a triangle. This rule states that the sum of aby two sides of the triangle has to be greater than the length of the third side.

First set: 11, 4, 9

`\begin{gathered} 11+4>9 \\ 15>9 \end{gathered}`
`\begin{gathered} 4+9>11 \\ 13>11 \end{gathered}`
`\begin{gathered} 9+11>4 \\ 20>4 \end{gathered}`

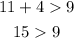
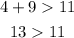
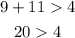
As you can see the first two sums follow the rule but the third one doesn't, so this set of lengths cannot side lengths of a triangle.

Second set: 13, 10, 10

`\begin{gathered} 13+10>10 \\ 23>10 \end{gathered}`
`\begin{gathered} 10+10>13 \\ 20>13 \end{gathered}`
`\begin{gathered} 10+13>10 \\ 23>10 \end{gathered}`

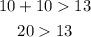
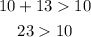
This set of lengths can be side lengths of a triangle.

Third set: 12, 18, 10

`\begin{gathered} 12+18>10 \\ 30>10 \end{gathered}`
`\begin{gathered} 18+10>12 \\ 28>12 \end{gathered}`
`\begin{gathered} 10+12>18 \\ 22>18 \end{gathered}`

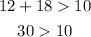
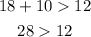
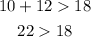
This set of lengths can be side lengths of a triangle.

Fourth set: 9.9, 4.8, 15.6

`\begin{gathered} 9.9+4.8>15.6 \\ 14,7>15.6 \end{gathered}`
`\begin{gathered} 4.8+15.6>9.9 \\ 20.4>9.9 \end{gathered}`
`\begin{gathered} 15.9+9.9>4.8 \\ 25.8>4.8 \end{gathered}`

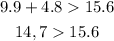
In the first sum, the sum of both sides is not greater than the length of the third side, so this set cannot be side lengths of a triangle.