In this case n = 8
p = 79% = 0.79
q = 1 - p = 1 - 0.79 = 0.21
x for the first question is 6
x for the second question is <=4, so it is the sum of the probabilities when x = 1, x =2, x = 3 and x = 4
Using the formula at the bottom:
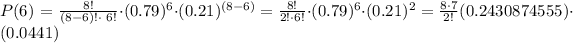
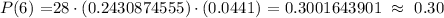
Probability of exactly 6 woman will purchase pet insurance
P(X = 6) = 0.30 = 30%
Probability of at least 4 men will purchase pet insurance (That means that 4 or less woman out of the 8 randomly selected will purchase pet insuranse):
P(X <= 4) = P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4) = 0.0659 = 6.59%