Given the roots/solutions of a quadratic equation as;
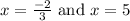
The general way of solving this kind of problem is by inserting/substituting it into the general form of factorized quadratic equation which is;
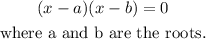
substituting the roots given in the question we have;
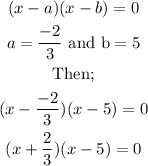
Then we can now expand to get the Quadratic equation.
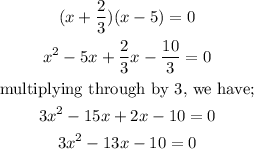
So, the quadratic equation with the roots/solutions x= -2/3 and x=5 is;
