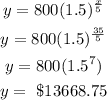Solution:
Given:
Using the exponential function formula,
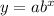
From the table, pick two points; (5,1200) and (10,1800)

Therefore, the exponential function is:
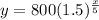
To complete the table,
when x = 20 years;
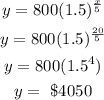
when x = 25 years;
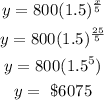
when x = 30 years;
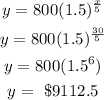
when x = 35 years;