Answer:
The length is 12 ft, the width is 4 ft and the height is 2 ft
Step-by-step explanation:
Here, we want to get the values of the dimensions of the box
The volume is simply the product of the length, width, and height
We have that as follows:
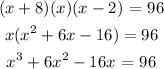
By plotting the function, we have 3 intercepts on the x-axis as shown below:
These intercepts are the solutions to the equation. We have the values as:
x = -6, x = -4 and x = 4
x cannot be -6 and -4 as dimension cannot be negative
Thus, we are left with 4
The side lengths are thus:
4 ft, (4+8) ft and (4-2) ft
These are 4 ft, 12 ft and 2 ft