From the question, we have the following parameters
μ = 1.015, σ = 0.13, n = 50, x-bar = 0.995
We will apply the above in the z-test formula below
![z=\frac{\bar{x}-\mu}{\frac{\sigma}{\sqrt[]{n}}}](https://img.qammunity.org/2023/formulas/mathematics/college/bqefrfb5c4zhs0vjts5lgjs1kij7yne2zk.png)
Therefore, we will then have;
![\begin{gathered} z=\frac{0.995-1.015}{\frac{0.13}{\sqrt[]{50}}} \\ z=\frac{-0.02}{\frac{0.13}{\sqrt[]{50}}} \\ z=-0.02*\frac{\sqrt[]{50}}{0.13} \\ z=-1.0879 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/jf1on2kcm26aq8apfy5p4kt2lohixonzg8.png)
Hence, we will find the probability of the above z score to get our answer. Using a z calculator, we will then have;
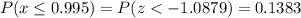
Answer: 0.1383