ANSWER
Step-by-step explanation
Given information
let the two numbers be x and y
According to the question provided, the two numbers add up to 50
x + y = 50 --------- equation 1
The next process is to maximize the product of the two numbers
From equation 1, we can determine the value of y
x + y = 50
y = 50 - x
Hence, the product of the two numbers is

To find the maximum of the above equation, we will need to differentiate first

The next step is to equate f'(x) to be zero

since x = 25, then we can now find the value of y
y = 50 - x
y = 50 - 25
y = 25
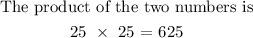
Therefore, the maximum possible value of their product is 625