Question

If two numbers add up to 50, what is the maximum possible value of their product?

Answer 1

Step-by-step explanation

Given information

let the two numbers be x and y

According to the question provided, the two numbers add up to 50

x + y = 50 --------- equation 1

The next process is to maximize the product of the two numbers

From equation 1, we can determine the value of y

x + y = 50

y = 50 - x

Hence, the product of the two numbers is

`\begin{gathered} f(x)=x(50\text{ - x)} \\ f(x)=50x-x^2 \end{gathered}`

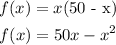
To find the maximum of the above equation, we will need to differentiate first

`f^(\prime)(x)\text{ = 50 - 2x}`

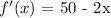
The next step is to equate f'(x) to be zero

`\begin{gathered} 0\text{ = 50 - 2x} \\ \text{subtract 50 from both sides} \\ 0\text{ - 50 = 50 - 50 - 2x} \\ -50\text{ = -2x} \\ \text{Divide both sides by -2} \\ \frac{\cancel{-50}\text{ 25}}{\cancel{-2}}\text{ = }\frac{\cancel{-2}x}{\cancel{-2}} \\ x\text{ =25} \end{gathered}`

since x = 25, then we can now find the value of y

y = 50 - x

y = 50 - 25

y = 25

`\begin{gathered} \text{The product of the two numbers is} \\ 25\text{ }*\text{ 25 = 625} \end{gathered}`

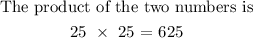
Therefore, the maximum possible value of their product is 625