Question

Vector C is 6.28 m long in a105° direction. Vector D is3.09 m long in a 233° direction.Find the magnitude of theirvector sum.

Answer 1

Answer:

The magnitude of the vector sum = 5.01 m

Explanations:

Step 1: Find the horizontal and vertical components of vector C

`\begin{gathered} \text{The horizontal component: C}_x=\text{ }6.28\cos 105 \\ C_x=\text{ }-1.625m \\ \text{The vertical componet: C}_y=\text{ 6.28}\sin 105 \\ C_y=\text{ }6.066m \end{gathered}`

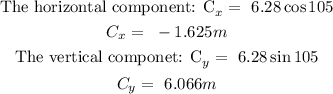
Step 2: Find the horizontal and vertical components of vector D

`\begin{gathered} \text{The horizontal component: D}_x=\text{ 3.09}\cos 233 \\ D_x=\text{ }-1.86m \\ \text{The vertical componet: D}_y=\text{ 3.09}\sin 233 \\ D_y=\text{ }-2.468m \end{gathered}`

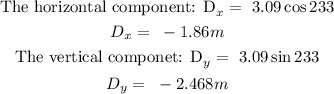
Step 3: The vector sum (A) is found by adding the x and y componets of vectors C and D

`\begin{gathered} A_x=C_x+D_x \\ A_x=\text{ -1.625 + (-1.86)} \\ A_x=\text{ }-3.485m \end{gathered}`
`\begin{gathered} A_y=C_y+D_y \\ A_y=\text{ 6.066+}(-2.468) \\ A_y=\text{ }3.598m \end{gathered}`

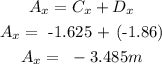
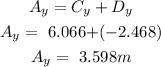
The vector sum is therefore:

`\begin{gathered} A=A_xi+A_yj \\ V\text{ = }-3.485i+3.598j \end{gathered}`

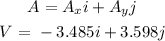
Step 4: The magnitude of the vector sum is therefore:

`\begin{gathered} |V|\text{ = }\sqrt[]{(-3.485)^2+(3.598)^2} \\ |V|\text{ = }\sqrt[]{25.09} \\ |V|\text{ = }5.01 \end{gathered}`

The magnitude of the vector sum = 5.01 m