Question

At what rate is his distance increasing from home plate when he is 20ft from second base

Answer 1

First, use the following diagram:

Take into account that red line is the distance from player to home at time t. Furthermore, distance d is the hypotenuse of a right triangle formed by d and two sides of the diamond.

Then, you have for d:

`d^2=90^2+x^2`

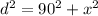
Next, derivate the previous expression related to time t:

`2d(d(d))/(dt)=2x(dx)/(dt)`

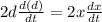
Next, consider that dx/dt = 21, (the speed of the player) and we need the value of d(d)/dt when x = 90ft - 20ft = 70ft.

Replace the prvious values into the expression the previous equation and solve for d(d)/dt, as follow:

`\begin{gathered} 21\cdot(d(d))/(dt)=2(70) \\ \frac{d(d)}{\mathrm{d}t}=(140)/(21)=6.666667 \end{gathered}`

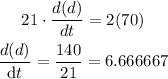
Next, by rounding the answer, you obtain:

6.666667 ft/s ≈ 6.67 ft/s