First, use the following diagram:
Take into account that red line is the distance from player to home at time t. Furthermore, distance d is the hypotenuse of a right triangle formed by d and two sides of the diamond.
Then, you have for d:
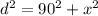
Next, derivate the previous expression related to time t:
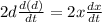
Next, consider that dx/dt = 21, (the speed of the player) and we need the value of d(d)/dt when x = 90ft - 20ft = 70ft.
Replace the prvious values into the expression the previous equation and solve for d(d)/dt, as follow:
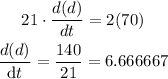
Next, by rounding the answer, you obtain:
6.666667 ft/s ≈ 6.67 ft/s