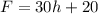Remember the equation of a line in slope-intercept form:

Where y is the dependent variable, x is the independent variable, m is the slope of the line and b is the initial value of y when x=0.
In this case, the dependent variable is F (the total fee), the independent variable is h (time in hours), the initial value b is $20 and the rate of change m is equal to 30.
Therefore, the linear equation that represents a fee equal to $30 per hour plus an initial fee of $20, is: