Looking at the constrains, we have that x and y must be positive values.
Also, if we divide the first inequality by two, we have that the sum of x and y must be greater than or equal 3.
Therefore, for the equation Z = 5x + 2y, the maximum value would be infinity, since the values of x and y can grow to any positive value and still satisfy the constrains.
If the question is asking "minimum value" instead of "maximum value", we can find it by using x = 0 and y = 3 (we choose the minimum possible value for x, because its coefficient in the equation Z = 5x + 3y is bigger, therefore it has the greater impact in the function value)
In this case, the minimum value of Z would be:
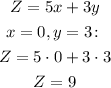
There is no option for this value of Z.
So instead of calculating the minimum value, let's change the sign of the inequality 2x + 2y >= 6 for 2x + 2y <= 6.
In this case, we should maximize x, since it has the greater coefficient in the equation for Z.
So we should choose x = 3 and y = 0:
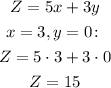
Then, in this case, using the inequality 2x + 2y <= 6, the correct option would be the first one (15).