Question

Solve for c.

a (b – c) = d


a) c= d - ab/a

b) c= ab – d/b

c) c= ab – d/a

d) c= ab + d/а

Answer 1

The given figure

There is a circle of radius of 10

Then the hypotenuse of the right triangle is the radius of the circle = 10

Since one leg of the triangle is 6

Then we can use the Pythagoras Theorem to find AE, then multiply it by 2 to find AB

Since < AEM = 90 degrees, then

`AM^2=AE^2+EM^2`

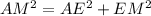
M is the center of the circle

Since AM = 10, ME = 6, then

`\begin{gathered} 10^2=AE^2+6^2 \\ 100=AE^2+36 \end{gathered}`

Subtract 36 from both sides

`\begin{gathered} 100-36=AE^2+36-36 \\ 64=AE^2 \end{gathered}`

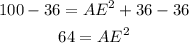
Take a square root for both sides

`\begin{gathered} \sqrt[]{64}=\sqrt[]{AE^2} \\ 8=AE \end{gathered}`

Since DC is perpendicular to AB and passing through the center of the circle, then

DC bisects AB, which means E is the mid-point of AB

AE = EB = 8

AB = 8 + 8 = 16

AB = 16