We are asked to convert the repeating decimal to fraction
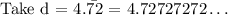

Step 1: Multiply both sides by 100 because there are two repeating digits
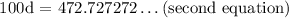
Step 2: Subtract the first equation from the second one

Therefore, the fractional form of the repeating decimal 4.7277272... is 52/11