Question

The sum of two number is negative fifteen, and one number is seven less than the other. Using the variables m and n to represent the two numbers, write a system of equations that describe the situation. Enter the equations below, separated by a comma. Next find the two numbers. Enter them below, separated by a comma.

Answer 1

The sum of two numbers is negative fifteen, and one number is seven less than the other. The two numbers are -4 and -11.

Step-by-step explanation:

Let m and n represent the two numbers.

From the given information, we can write the system of equations:

m + n = -15

m = n - 7

Solving this system of equations, we can substitute the expression for m from the second equation into the first equation:

n - 7 + n = -15

2n - 7 = -15

2n = -8

n = -4

Substituting the value of n back into the second equation:

m = (-4) - 7 = -11

Therefore, the two numbers are -4 and -11.

Answer 2

System of equation = m + n = -15, m - n = 7

The two numbers = -4, -11

Explanation

Let variables m and n represent the two numbers.

The sum of variables m and n is negative fifteen, This implies;

`m+n=-15----i`

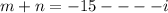
One number is seven less than the other implies;

`\begin{gathered} m-n=7----ii \\ \text{Where;} \\ m\text{ is the greater number and} \\ n\text{ is the lesser number} \end{gathered}`

Hence, the system of equations that describe the situation is

`\begin{gathered} m+n=-15----i \\ m-n=7-----ii \end{gathered}`

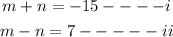
To find the two numbers, use the elimination method.

`\begin{gathered} (i)+(ii) \\ \Rightarrow m+m+n+(-n)=-15+7 \\ 2m=-8 \\ \text{Divide both sides by 2} \\ (2m)/(2)=-(8)/(2) \\ m=-4 \end{gathered}`

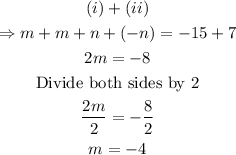
To get n, substitute m = -4 into (i)

`\begin{gathered} \text{Recall (i)} \\ m+n=-15---i \\ \Rightarrow-4+n=-15 \\ \text{Collect the like terms} \\ n=-15+4 \\ n=-11 \end{gathered}`

Therefore, the two numbers = -4, -11