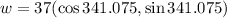ANSWER:
3rd option
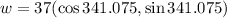
Explanation:
Given:
w = 35i - 12j
We know that the trigonometric form is given as follows:
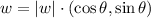
The first thing is to calculate the normal of the vector, just like this:
![\begin{gathered} |w|=\sqrt[]{35^2+(-12)^2} \\ |w|=\sqrt[]{1225+144} \\ |w|=\sqrt[]{1369} \\ |w|=37 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/zmxrbfiigt212jkv6b9ptf9zgk1npieos2.png)
Now, we calculate the value of the angle by means of the sine, just like this:
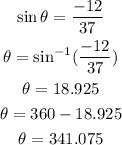
Therefore, the vector w in its trigonometric form is as follows: