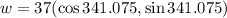Question

Which of the following represents vector w = 35i − 12j in trigonometric form?

Answer 1

3rd option

`w=37(\cos 341.075\degree,\sin 341.075\degree)`

Explanation:

Given:

w = 35i - 12j

We know that the trigonometric form is given as follows:

`w=|w|\cdot(\cos \theta,\sin \theta)`

The first thing is to calculate the normal of the vector, just like this:

`\begin{gathered} |w|=\sqrt[]{35^2+(-12)^2} \\ |w|=\sqrt[]{1225+144} \\ |w|=\sqrt[]{1369} \\ |w|=37 \end{gathered}`

Now, we calculate the value of the angle by means of the sine, just like this:

`\begin{gathered} \sin \theta=(-12)/(37) \\ \theta=\sin ^(-1)_{}\mleft((-12)/(37)\mright) \\ \theta=18.925 \\ \theta=360-18.925 \\ \theta=341.075\degree \end{gathered}`

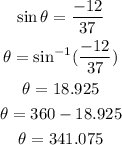
Therefore, the vector w in its trigonometric form is as follows:

`w=37(\cos 341.075\degree,\sin 341.075\degree)`