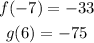Given the functions:
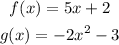
• You need to find:
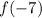
Then, you have to substitute this value of "x" into the function "f" and then evaluate:
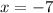
Then, you get:
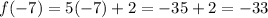
• Now you need to find:
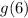
Substitute this value of "x" into the function "g" and then evaluate:
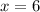
You get:
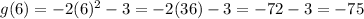
Hence, the answer is: