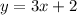Question

Given the two points (1,5) and (-2,-4), write a set of instructions, using formulas and the coordinates given, for your younger cousin that determines:1. slope of a line that passes through the 2 given points2. the equation of the line in slope intercept form (y=MX+b)

Answer 1

The slope of the line between the two points is;

`m=3`

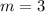
the slope-intercept form of the line joining the two points is;

`y=3x+2`

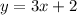
Step-by-step explanation:

Given the points;

`\begin{gathered} (1,5) \\ \text{and} \\ (-2,-4) \end{gathered}`

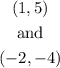
1.

We want to find the slope, using the coordinates;

`\begin{gathered} m=(y_2-y_1)/(x_2-x_1)=(-4-5)/(-2-1)=(-9)/(-3) \\ m=3 \end{gathered}`

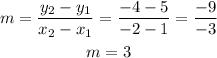
The slope of the line between the two points is;

`m=3`

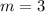
2.

Writing the equation in slope-intercept form;

`y=mx+b`

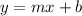
Let us substitute the slope and the coordinates of a point into the point-slope form of a linear equation;

`\begin{gathered} y-y_1=m(x-x_1) \\ m=3 \\ (x_1,y_1)=(1,5) \\ y-5=3(x-1) \\ y-5=3x-3 \\ y=3x-3+5 \\ y=3x+2 \end{gathered}`

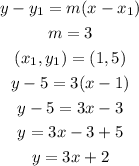
Therefore, the slope-intercept form of the line joining the two points is;

`y=3x+2`