Question

Determine any possible functions h and g, where h cannot equal g, but that h is the derivative of g, and g is the derivative of h. If it's not possible, explain why not.

Answer 1

Hello there. To solve this question, we'll have to remember some properties about functions and derivatives.

We want to determine any possible functions h and g, where h cannot equal g, but knowing that h is the derivative of g and g is the derivative of h.

Mathematically, we have that

`h^(\prime)(x)=g(x)\wedge h(x)=g^(\prime)(x)\text{ }`

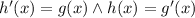
The way we can solve this is to consider that both h and g are twice differentiable, hence you differentiate both sides of the first expression to get:

`h^(\prime)^(\prime)(x)=g^(\prime)(x)`

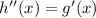
But knowing g'(x) is h(x), we get

`h^(\prime)^(\prime)(x)=h(x)`

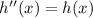
Subtract h(x) on both sides of the equation

`h^(\prime)^(\prime)(x)-h(x)=0`

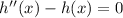
This is a second order linear homogeneous differential equation.

To solve it, assume that

`h(x)=e^(\lambda x)`

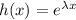
For a fixed constant λ

Taking its derivative twice, we get

`\begin{gathered} h^(\prime)(x)=\lambda\cdot e^(\lambda x) \\ \\ \Rightarrow h^(\prime)(x)=\lambda^2\cdot e^(\lambda x) \end{gathered}`

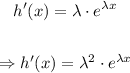
Plugging this into our equation, we get

`\lambda^2\cdot e^(\lambda x)-e^(\lambda x)=0`

Factor the exponential term

`e^(\lambda x)\cdot(\lambda^2-1)=0`

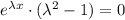
Since we know that

`e^(\lambda x)>0\text{ for any }\lambda\in\mathbb{C}`

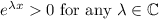
We get that

`\lambda^2-1=0`

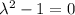
It is called the characteristic equation for this differential equation.

Solving it gives us:

`\lambda=1\text{ and }\lambda=-1`

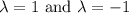
Therefore the solutions to this equation are

`h(x)=e^x\text{ and }h(x)=e^(-x)`

But since this is a linear equation, any finite combination of these solutions are solutions to it, therefore we say that

`h(x)=c_1\cdot e^x+c_2\cdot e^(-x)`

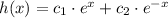
Is the general solution to this equation for any real constants c1 and c2.

Taking the derivative of this function, we'll see that

`g(x)=h^(\prime)(x)=c_1\cdot e^x-c_2\cdot e^(-x)`

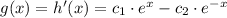
And the only case in which g(x) = h(x), that is what we don't want to have, is when

`\begin{gathered} g(x)=h(x) \\ \\ c_1\cdot e^x-c_2\cdot e^(-x)=c_1\cdot e^x+c_2\cdot e^(-x) \\ \\ c_2=-c_2=0 \end{gathered}`

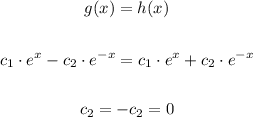
So it is possible to find infinitely many functions h and g of x satisfying this condition, as long c_2 is not equal to zero.

Take, for example, the solution:

`\begin{gathered} h(x)=3e^x+4e^(-x) \\ \\ g(x)=3e^x-4e^(-x) \end{gathered}`

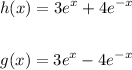
They are not equal, but satisfies the properties:

`\begin{gathered} h(x)=g^(\prime)(x) \\ g(x)=h^(\prime)(x) \end{gathered}`

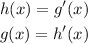
As wanted.

Another way of solving is: Add the conditions as follows

`h(x)+g(x)=h^(\prime)(x)+g^(\prime)(x)`

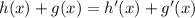
Now make the following substitution:

`f(x)=h(x)+g(x)`

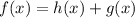
Since the differential operator is linear, it is true that

`f^(\prime)(x)=h^(\prime)(x)+g^(\prime)(x)`

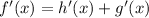
Hence we have that

`f(x)=f^(\prime)(x)`

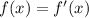
This is a first order linear homogeneous differential equation, but it is also a separable equation, that we can solve as:

Divide both sides of the equation by f(x) (knowing it is not identically equal to zero)

`(f'(x))/(f(x))=1`

Integrate both sides with respect to x, such that you get

`\int(f'(x))/(f(x))\,\mathrm{d}x=\int1\,\mathrm{d}x`

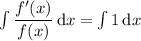
The left hand side of the integral equation can be calculated knowing that

`\int\frac{\mathrm{d}x}{x}=\ln|x|+C,C\in\mathbb{R}`

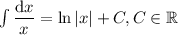
Hence we get

`\ln|f(x)|+C`

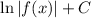
For the right hand side, we have the integral of a power of x. Remember that

`1=x^0`

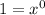
Therefore applying the power rule:

`\int\,x^n\,\mathrm{d}x=(x^(n+1))/(n+1)+C,\text{ }n\text{ not equal to }-1`

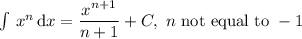
We get that

`\int1\,\mathrm{d}x=\int x^0\,\mathrm{d}x=(x^(0+1))/(0+1)+C_1=x+C_1`

Hence the equation gives us

`\ln|f(x)|+C=x+C_1`

Subtract C on both sides of the equation

`\begin{gathered} \ln|f(x)|=x+C_1-C \\ \\ \ln|f(x)|=x+K_1 \end{gathered}`

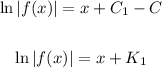
K_1 is another arbitrary constant.

Raise both sides of the equation as a power of e, as follows:

`\begin{gathered} \exp(\ln|f(x)|)=\exp(x+K_1) \\ \\ |f(x)|=K\exp(x)=Ke^x \end{gathered}`

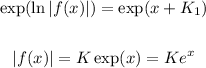
Here we applied the property of powers:

`e^(a+b)=e^a\cdot e^b`

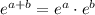
Since e^(K_1) is another constant, we called it K.

In this case, since it is a modular equation for f(x), we say that K must be a positive constant.

Returning to the definition, we see that

`h(x)+g(x)=Ke^x`

Making g(x) = h'(x), we have another equation

`h(x)+h^(\prime)(x)=Ke^x`

This time it is not a homogeneous equation, although it can be solved in a very similar way. The solution will be

`Ae^x+Be^(-x)`

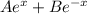
Just as we found before, for constants A and B.

We perform the same argument to say that h(x) will only be equal to g(x) if B = 0, therefore it is possible to find functions of this form satisfying these properties.