a) We have to draw a tree diagram for the situation.
As it has a probability of 41% of passing, there is a probability of 59% of failing.
He only takes another exam if he fails.
b) We have to calculate the probability that James will pass the actuarial exam.
To do that, we look at each of the branches that end in PASS.
The first branch is P, that means he passes in the first attempt. It has a probability of 0.41.
The second branch is FP, that means he fail the first exam and pass the second. It has a probability of 0.59*0.41=0.2419.
The third branch is FFP, that means he failed the first and second exams, and he passes in the third exam. It has a probability of 0.59*0.59*0.41=0.1427.
The probability of James of meeting his goal is equal to the sum of the probabilities of this branches:
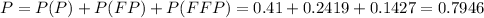
Probability of passing the actuarial exam = 0.7946.