a)
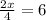
Solution: we can multiply x by 2 and divide by 4, so to solve for x, we can multiply bout sides of the eqution by 4/2 so:
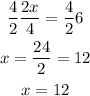
b)

first we can multiply by 4 so:
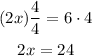
and now we can divide by 2 so:
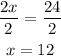
c)
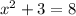
so we can rest 3 un bout sides of the equation:
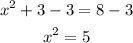
Now we can use the square root to solve for x so:
![\begin{gathered} \sqrt[]{x^2}=\sqrt[]{5} \\ x=\sqrt[]{5} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/xfivdk4lt8zibfk2babzeqb2kaaes3675y.png)