Question

Find the average rate of change of f(x) = √x+2/x^2 -3 from x1 = 2 to x2 = 7.

Answer 1

The formula for the average rate of change between two points on a function is:

`r=\frac{f(x_2)-f(x_1)_{}}{x_2-x_1}`

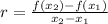
Since we want between:

`\begin{gathered} x_1=2 \\ x_2=7 \end{gathered}`

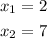
We need to first calculate the values of the funciton in these points:

`\begin{gathered} f(x_1)=f(2)=\frac{\sqrt[]{2+2}}{2^2-3}=\frac{\sqrt[]{4}}{4-3}=(2)/(1)=2 \\ f(x_2)=f(7)=\frac{\sqrt[]{7+2}}{7^2-3}=\frac{\sqrt[]{9}}{49-3}=(3)/(46) \end{gathered}`

Now, we input these into the formula:

`r=\frac{f(x_2)-f(x_1)_{}}{x_2-x_1}=((3)/(46)-2)/(7-2)=((3-2\cdot46)/(46))/(5)=((3-92)/(46))/(5)=((-89)/(46))/(5)=-(89)/(46)\cdot(1)/(5)=-(89)/(230)`

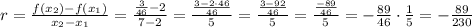
Thus, the average rate of change is -89/230.