Question

The weights for a group of 18-month-old girls are normally distributed with a mean of 24.8 pounds and a standard deviation of 2.9 pounds. Use the given table to find the percentage of 18-month-old girls who weigh between 19.1 and 23.6 pounds. _ % of 18- month-old girls weigh between 19.1 and 23.6 pounds.

Answer 1

Given:

The weight of 18-month-old girls is normally distributed with a mean of 24.8 pounds and a standard deviation of 2.9 pounds. The table of z-score percentile is given.

Required:

Find the percentile of the 18-month-old girl whose weight is between 19.1 and 23.6 pounds.

Step-by-step explanation:

First, find the z-score by using the formula:

`z-score=\frac{data\text{ item-mean}}{standard\text{ deviation}}`
`\begin{gathered} z_(19.1)=(19.1-24.8)/(2.9) \\ z_(19.1)=(-5.7)/(2.9) \\ z_(19.1)=-1.9655 \\ z_(19.1)\approx-2.0 \end{gathered}`
`\begin{gathered} z_(23.6)=(23.6-24.8)/(2.9) \\ z_(23.6)=(-1.2)/(2.9) \\ z_(23.6)=-0.4137 \\ z_(23.6)\approx-0.41 \end{gathered}`

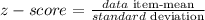
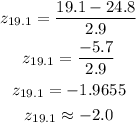
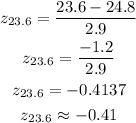
Now by using the table find the percentile corresponding to the z-score.

The percentile corresponds to z-score -2.0 = 2.28

The percentile corresponds to z-score -0.41 = 34.46

Find the difference between the percentile =

`\begin{gathered} 34.46-2.28=32.18 \\ \approx32.18 \end{gathered}`

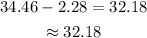
Thus the 18-month-old girl's weight between 19.1 and 23.6 pounds is 32.18%.

Final Answer:

32.18%