Answer:
2.29 rad
Explanation:
The terminal arm of an angle in standard position passes through the point:
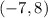
For an angle in standard position, its angle in degrees:
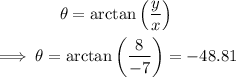
Since (-7, 8) is in Quadrant II:
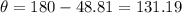
Finally, convert the result to radians:
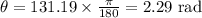
The radian value of the angle in the interval (0, 2π) correct to the nearest hundredth is 2.29 radians.