Question

A student wants to know how far above the ground the top of a leaning flagpole is. At high noon, when the sun is almost directly overhead, the shadow cast by the pole is 7 ft long. The student holds a plumb bob with a string 2 feet long up to the flagpole and determined that the point of the plumb bob touches the ground 11 inches from the base of the flagpole. How far above the ground is the top of the pole?

Answer 1

Since the sun is almost directly overhead, then we can say that we have two right triangles that are similar.

So, we can formulate the following equation:

`\begin{gathered} (h1)/(b1)=(h2)/(b2)\text{ (h1: 2 ft, b1: 11 in=0.92 ft, h2: height of the top of the pole, b2: shadow of the pole )} \\ \frac{2\text{ ft}}{0.92\text{ ft}}=\frac{h2}{7\text{ ft}}\text{ (Replacing)} \\ \frac{2\text{ ft}}{0.92\text{ ft}}\cdot7\text{ ft= h2 (Multiplying by 7 ft on both sides of the equation)} \\ 15.22\text{ ft = h2 (Dividing and multiplying )} \end{gathered}`

The height is 15.21 ft.

Converting the answer to inches, we have:

`15.22ft\cdot\frac{12\text{ in}}{1\text{ ft}}=182.6\text{ in}`

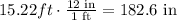
The answer is 183 inches (Rounding to the nearest inch)