Question

Please help:)find xits a right triangle so side AT and side AP are congruent

Answer 1

EXPLANATION

Given the triangle on the circle, we can see that the angle A is a 90 degrees angle, so we can apply the Law of Sines as shown as follows:

Law of Sines:

`(A)/(\sin A)=(B)/(\sin B)`

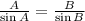
In this case, A= 23sqrt(2), Sin A= Sin 90 = 1, B=x , Sin B = Sin 45

Replacing terms:

`\frac{23\sqrt[]{2}}{1}=(x)/(\sin 45)`

Switching sides:

`(x)/(\sin 45)=23\sqrt[]{2}`

Multiplying both sides by Sin 45:

`x=\sin 45\cdot23\cdot\sqrt[]{2}`

Solving Sin 45:

`x=\frac{\sqrt[]{2}}{2}\cdot3\cdot\sqrt[]{2}`

Applying the square root properties and grouping the fractions:

`x=(3)/(2)\sqrt[]{(2)^2}`

Simplifying the square root with the power:

`x=(3)/(2)\cdot2=3`

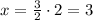
The answer is x=3