EXPLANATION
Given the triangle on the circle, we can see that the angle A is a 90 degrees angle, so we can apply the Law of Sines as shown as follows:
Law of Sines:

In this case, A= 23sqrt(2), Sin A= Sin 90 = 1, B=x , Sin B = Sin 45
Replacing terms:
![\frac{23\sqrt[]{2}}{1}=(x)/(\sin 45)](https://img.qammunity.org/2023/formulas/mathematics/high-school/ldl8jnd2za20x5ybaw8isrwkxba84ppll3.png)
Switching sides:
![(x)/(\sin 45)=23\sqrt[]{2}](https://img.qammunity.org/2023/formulas/mathematics/high-school/cncsx7ilxq6stwwf1j3qdwjgur5q6b4n3t.png)
Multiplying both sides by Sin 45:
![x=\sin 45\cdot23\cdot\sqrt[]{2}](https://img.qammunity.org/2023/formulas/mathematics/high-school/uxdpvvkq1yy2dct6mjpr4ztnumei0mge7g.png)
Solving Sin 45:
![x=\frac{\sqrt[]{2}}{2}\cdot3\cdot\sqrt[]{2}](https://img.qammunity.org/2023/formulas/mathematics/high-school/7mnvs9hetmjwds9s7co6p0o4fx8iq59nxp.png)
Applying the square root properties and grouping the fractions:
![x=(3)/(2)\sqrt[]{(2)^2}](https://img.qammunity.org/2023/formulas/mathematics/high-school/ws0kubgsbgsweu5gtqxf88uj31fmljaeaj.png)
Simplifying the square root with the power:
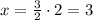
The answer is x=3