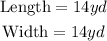Question

The perimeter of a rectangle is 56 yards. What are the dimensions of the rectangle with maximumarea?

Answer 1

Let the length of the rectangle be "x" and the width be "y".

We know the formula for the area of a rectangle:

`\begin{gathered} A=\text{length}*\text{width} \\ A=xy \end{gathered}`

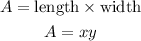
We know the formula for the perimeter of a rectangle:

`\begin{gathered} \text{Perimeter}=2(length+width) \\ 56=2(x+y) \\ (56)/(2)=x+y \\ x+y=28 \end{gathered}`

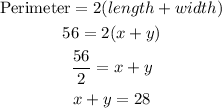
Let's solve for "x" in the perimeter equation to get:

`x=28-y`

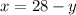
Now, we will substiute this into the Area equation. Shown below:

`\begin{gathered} A=xy \\ A=(28-y)y \\ A=28y-y^2 \end{gathered}`

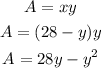
To find the maximum area, we need to differentiate "A" equation and set it equal to 0 to find the value of "y" for which "A" is maximum. The steps are shown below:

`\begin{gathered} A=28y-y^2 \\ A^(\prime)=28-2y \\ 28-2y=0 \\ 2y=28 \\ y=(28)/(2) \\ y=14 \end{gathered}`

The corresponding "x" value is:

`\begin{gathered} x=28-y \\ x=28-14 \\ x=14 \end{gathered}`

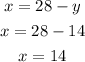
Thus, the rectangle with the maximum area is the one with dimensions:

`\begin{gathered} \text{Length}=14yd \\ \text{Width}=14yd \end{gathered}`