Answer:
Function A has the greater average rate of change over the interval [1, 2]
Step-by-step explanation:
Given the below functions and interval [1, 2};

Note that the below formula can be used to determine the average rate of change over an interval [a, b};
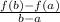
Average rate of change of Function A:
Given the interval [1, 2] where a = 1 and b = 2, let's go ahead and determine g(a), g(b), and the average rate of change of Function A as seen below;
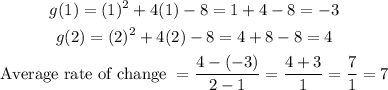
So the average rate of change of Function A is 7
Average rate of change of Function B:
Given the interval [1, 2] where a = 1 and b = 2, let's go ahead and determine h(a), h(b), and the average rate of change of Function B as seen below ;
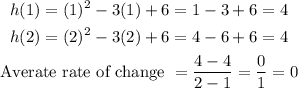
So the average rate of change of Function B is 0
If we compare the average rate of change of the two functions, we can see that Function A has the greater average rate of change over the interval [1, 2]