Question

How do I calculate and compare the rate of change of two functions or an interval?

Answer 1

Function A has the greater average rate of change over the interval [1, 2]

Step-by-step explanation:

Given the below functions and interval [1, 2};

`\begin{gathered} \text{Function A: }g(x)=x^2+4x-8 \\ \text{Function B: }(x)=x^2-3x+6 \end{gathered}`

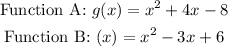
Note that the below formula can be used to determine the average rate of change over an interval [a, b};

`(f(b)-f(a))/(b-a)`

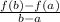
Average rate of change of Function A:

Given the interval [1, 2] where a = 1 and b = 2, let's go ahead and determine g(a), g(b), and the average rate of change of Function A as seen below;

`\begin{gathered} g(1)=(1)^2+4(1)-8=1+4-8=-3 \\ g(2)=(2)^2+4(2)-8=4+8-8=4 \\ \text{Average rate of change }=(4-(-3))/(2-1)=(4+3)/(1)=(7)/(1)=7 \end{gathered}`

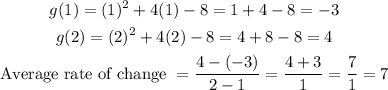
So the average rate of change of Function A is 7

Average rate of change of Function B:

Given the interval [1, 2] where a = 1 and b = 2, let's go ahead and determine h(a), h(b), and the average rate of change of Function B as seen below ;

`\begin{gathered} h(1)=(1)^2-3(1)+6=1-3+6=4 \\ h(2)=(2)^2-3(2)+6=4-6+6=4 \\ \text{Averate rate of change }=(4-4)/(2-1)=(0)/(1)=0 \end{gathered}`

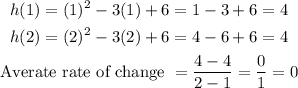
So the average rate of change of Function B is 0

If we compare the average rate of change of the two functions, we can see that Function A has the greater average rate of change over the interval [1, 2]