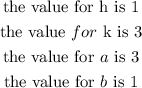Solution:
Given the graph of the ellipse as shown below:
The standard form of an ellipse whose major axis is parallel to thex-axis is
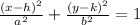
The length of the major axis equals 2a.
Thus,
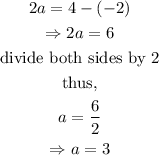
We can determine the center (h,k) using the midpoint formula expressed as
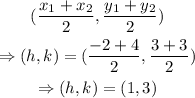
The co-vertices of the graphed ellipse is
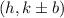
This implies that
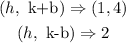
Thus, when
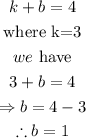
Hence,