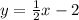Question

Find an equation for the line perpendicular to the line 4x + 2y = 6 having the same y-intercept as 2x + y = -2.

Answer 1

Rewrite equation 4x + 2y = 6 into the form y=mx+c, where m is the slope and c is the y intercept.

`\begin{gathered} 2y=-4x+6 \\ y=(-4x)/(2)+(6)/(2) \\ y=-2x+3\text{ ---(1)} \end{gathered}`

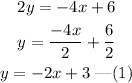
Comparing equation (1) with y=mx+c, we get m=-2.

Hence, the slope of the line 4x + 2y = 6 is m=-2

So, the slope of a line perpendicular to 4x + 2y = 6 is,

`\begin{gathered} M=(-1)/(m) \\ M=(-1)/(-2) \\ =(1)/(2) \end{gathered}`

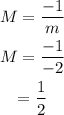
Therefore, the the slope of a line perpendicular to 4x + 2y = 6 is M=1/2.

Now, rewrite th equation 2x+y=-2 into the form y=mx+c.

`y=-2x-2\text{ ---(2)}`

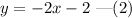
Comparing equation (2) with y=mx+c, the y intercept of line 2x+y=-2 is c=-2.

Now, the equation of a line with slope M=1/2 and y intercept c=-2 is given by,

`\begin{gathered} y=Mx+c \\ y=(1)/(2)x-2 \end{gathered}`

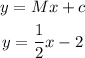
Therefore, the equation of a line perpendicular to the line 4x + 2y = 6 having the same y-intercept as 2x + y = -2 is,

`y=(1)/(2)x-2`