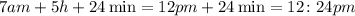Question

I need help with this homework questionI keep coming up with the wrong answer.

Answer 1

We can represent the exponential decay function as

`f(t)=f(0)e^(kt)`

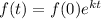
where f(0) is the initial value of the function and k is a constant.

Since we know the half-life of that liquid is 2.2 hours, f(2.2) equals f(0)/2. So, we have:

`\begin{gathered} (f\mleft(0\mright))/(2)=f(0)e^(2.2k) \\ \\ (1)/(2)=e^(2.2k) \\ \\ \ln (1)/(2)=\ln (e^(2.2k)) \\ \\ \ln 0.5=2.2k \\ \\ k=(\ln 0.5)/(2.2) \end{gathered}`

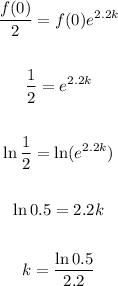
Thus, we can use this result and f(0) = 2.25 (ml) to determine the function f(x):

`f(t)=2.25\cdot e^{(\ln0.5)/(2.2)t}`

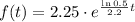
Thus, to find the number of hours passed after the liquid was administrated when it decreases to 0.41 ml, we need to make f(t) = 0.41 and find t:

`\begin{gathered} 0.41=2.25\cdot e^{(\ln0.5)/(2.2)t} \\ \\ (0.41)/(2.25)=e^{(\ln0.5)/(2.2)t} \\ \\ \ln (0.41)/(2.25)=\ln e^{(\ln0.5)/(2.2)t} \\ \\ (\ln 0.5)/(2.2)t=\ln (0.41)/(2.25) \\ \\ t=(2.2\cdot\ln (0.41)/(2.25))/(\ln 0.5) \\ \\ t\cong5.40370 \end{gathered}`

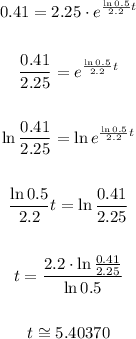
So approximately 5.404 hours passed since the liquid was administrated at 7:00 am. Then, to find the hour and minutes, let's convert:

`5.404h=5h+0.404h=5h+0.404\cdot60\min \cong5h+24\min`

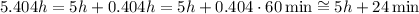
Thus, adding this result to 7:00 am, we find:

`7am+5h+24\min =12pm+24\min =12\colon24pm`