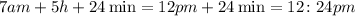We can represent the exponential decay function as
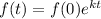
where f(0) is the initial value of the function and k is a constant.
Since we know the half-life of that liquid is 2.2 hours, f(2.2) equals f(0)/2. So, we have:
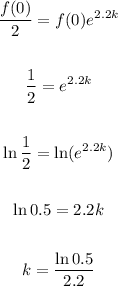
Thus, we can use this result and f(0) = 2.25 (ml) to determine the function f(x):
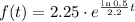
Thus, to find the number of hours passed after the liquid was administrated when it decreases to 0.41 ml, we need to make f(t) = 0.41 and find t:
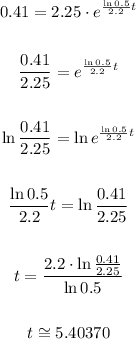
So approximately 5.404 hours passed since the liquid was administrated at 7:00 am. Then, to find the hour and minutes, let's convert:

Thus, adding this result to 7:00 am, we find: