Question

While an elevator of mass 809 kg moves downward, the tension in the supporting cable is a constant 7730 N. Between t = 0 and t = 4.00 s, the elevator’s displacement is 5.00 m downward. What is the elevator’s speed at t = 4.00 s?

Answer 1

Given,

The mass of the elevator, m=809 kg

The tension in the support cable, T=7730 N

The time instant at which the speed of the elevator is needed to be found out, t=4.00 s

The displacement of the elevator, d=5.00 m

As the elevator is moving downwards, the net force on the elevator is directed downwards.

The net force on the elevator is given by,

`\begin{gathered} F_n=ma \\ =mg-T \end{gathered}`

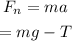
Where g is the acceleration due to gravity.

On substituting the known values,

`\begin{gathered} 809* a=809*9.8-7730 \\ \Rightarrow a=(198.2)/(809) \\ =0.245\text{ m/s}^2 \end{gathered}`

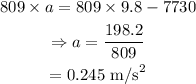
From the equation of motion,

`\begin{gathered} d=vt-(1)/(2)at^2 \\ \Rightarrow vt=d+(1)/(2)at^2 \\ \Rightarrow v=(1)/(t)(d+(1)/(2)at^2) \end{gathered}`

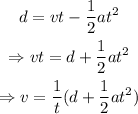
On substituting the known values in the above equation,

`\begin{gathered} v=(1)/(4)(5+(1)/(2)*0.245*4^2) \\ =(1)/(4)(5+1.96) \\ =1.74\text{ m/s} \end{gathered}`

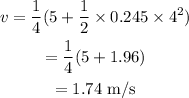
The speed of the elevator at t=4.00 s is 1.74 m/s