Given,
The mass of the elevator, m=809 kg
The tension in the support cable, T=7730 N
The time instant at which the speed of the elevator is needed to be found out, t=4.00 s
The displacement of the elevator, d=5.00 m
As the elevator is moving downwards, the net force on the elevator is directed downwards.
The net force on the elevator is given by,
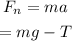
Where g is the acceleration due to gravity.
On substituting the known values,
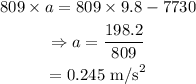
From the equation of motion,

On substituting the known values in the above equation,
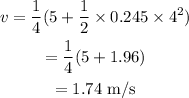
The speed of the elevator at t=4.00 s is 1.74 m/s