THIS IS HIGH SCHOOL CALCULUS PROBLEM! MUST SHOW ALL THE JUSTIFICATION!!!

Question

asked Oct 23, 2023 163k views

1 Answer

Yiming · Answer 1 · 2023-10-28T03:14:13+0000

Given the graph of the function "f", you need to find the approximate output value:

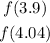
$\begin{gathered} f(3.9) \\ f(4.04) \end{gathered}$

Notice that both values are closed to:

Therefore, you can use this formula:

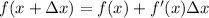
$f(x+\Delta x)=f(x)+f^(\prime)(x)\Delta x$

In this case, you can approximate that:

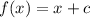
Where "c" is a constant.

Its derivative is:

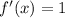
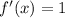
$f^(\prime)(x)=1$
$f^(\prime)(x)=1$

(a) In order to find:

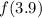
You need to use:

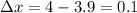
$\Delta x=4-3.9=0.1$

Then, using the formula, you get:

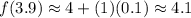
$f(3.9)\approx4+(1)(0.1)\approx4.1$

(b) And for the other value:

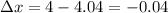
$\Delta x=4-4.04=-0.04$

Then:

$f(4.04)\approx4+(1)(-0.04)\approx3.96$

Hence, the answers are:

(a)

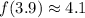
$f(3.9)\approx4.1$

(b)

$f(4.04)\approx3.96$