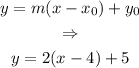Question

2) write the equation of a line that passes through the point ( 4, 5) and is perpendicular to a line that passes through the points (-6, 8) and (10,0).

Answer 1

The general equation of a line with slope m that passes through a point (x_0,y_0) is:

`y=m(x-x_0)+y_0`

On the other hand, two lines are perpendicular if their slopes m_1 and m_2 satisfy the contition:

`m_1\cdot m_2=-1`

Using the slope formula, determine the slope of the line that passes through the points (-6,8) and (10,0):

`m_2=(8-0)/(-6-10)=(8)/(-16)=-(1)/(2)`

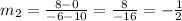
A line perpendicular to that, will have a slope of:

`m_1=-(1)/(m_2)=-(1)/((-(1)/(2)))=2`

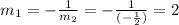
Substitute the value for m_1 and the coordinates (4,5) in the general equation for a line with a given slope that passes through a given point:

`\begin{gathered} y=m(x-x_0)+y_0 \\ \Rightarrow \\ y=2(x-4)+5 \end{gathered}`